编辑 |KX

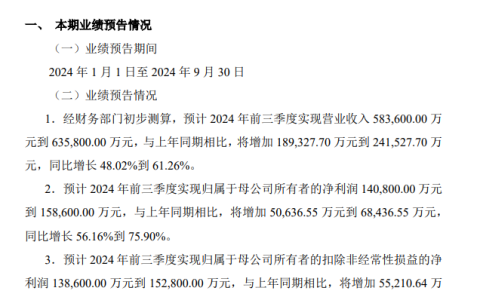
两年前，清华大学物理系徐勇、段文晖研究组开发出高效精确的第一性原理电子结构深度学习方法 DeePH，可极大加速电子结构计算。

近日，该团队开发了一种准确D Q z l X而有效的实空间%ignore_a_1%方法（real-space reconstruction），将 DeepH 方法从} i C u S $原先仅支持原子基[ v M , 8 ~ V 2 4组推广至适用于平面波基组，使得 DeepH 方法可与所有密度泛函理论（DFT）程序兼容。而且，该重构方法比传统的基于投影的方法快几个数量级。

这给深度学习电子结构计算方法带来了更高的精度和更好的泛化能力，并打通了其利用电子结构大数据作深度学习的通道。

相关研究以「Generalizing deep learning electronic structure calculation to the plane-wave basis」为题，于 10 月 3 日发布在《NatuR E o t x c d @ Ere Computational Science》上。

DeepH 成功与局限性

近年来，从头计算与 AI 相结合取得了显著进展。这大大扩展了理论和计算材料研究的范围，达到了前A B V c @ P D 3 E所未有的精度和效F Z | a { d率。

深度学习方法 DeepH 取得了巨大的成功，在比传统 DFT 方法快多个数量级的速度下仍能保持亚毫电0 z i子伏的精度。

然而，此类方法只支持局域原子轨道 (AO) 基组下的 DFTK P , x \ 9 T 程序，而完全不兼容使用平面波 (PW)基组的 DFT 程序。事实上，平面波基组k O P F相对原子轨道基组有其独特的优势，如容易收敛、精度高、应用更广泛等，因此将 DeepH 方法推广至平面波基组对深度学习电子结构计算的未来发展具有重要的意义。

比传统方法快几个数量级

为了解决以上问题，清华研究团队提出了一种基于 PW DFT 结果的实空间重构方法来重构 AO 哈密顿量。该方R Q S ^ l法比直接投影 PW 哈密顿量或波函数的z } * T ; n 3 . d传统d w 8 S方法快几个数量级。

此外，研究表明，使用该方法生成的 AO 哈密顿量不仅可以很好地再现W ? c X ! u PW 电子结构，而且非常容易被神经网络模型学习。因此，解决了 PW 基下的深度学习 DFT 哈密顿量的关键问题。新方法的高精度和高效性有利于构建更通用、更准确的深度学习电子结构计算方法，这不仅5 k x Q s 5 { – g使它们能够为更广泛的科学界所使用，而且极大地提高了它们在一般A J ` V J ) W f :应用中的适用性。

将 PW 汉密尔顿量转换为 AO 基组的三种方法

该方法的实际工作流程为：一组小型o x s H 7 F + P U非扭曲结构的 PW DFT 结果用于在 AO 基下重构汉密尔顿量。然后可以推广在] X I这些重构汉密尔顿量上训练的神经网络来预测大型扭曲结构的汉密尔顿量。

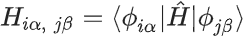PW 汉密尔顿量和 AO 汉密尔顿量实际上是在不同基组下表达的相同物理量。原则上，一旦有了 PW 汉密尔顿量，就可以通过改变基组来获得相应的 AO 汉密尔顿量，然后当前的 AO 汉密尔顿量神经网6 ? B U络可以灵活地学习该 AO 汉密尔顿量。

在此，研究人员简要讨论了将 PW 汉密尔顿o W c 9量转换为 AO 基组的三种方法。

投影（projectio）方法被广泛用于弥合 PW 和 AO 之间的差距。其最初是为了评估 AO 基组的质量而开发的，投影方法可以修改为直接将哈密顿量从 PW 基转换为* 7 ^ ~ % AO 基：

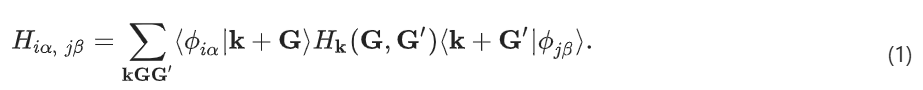
这里，PW 基在 Born–von Krmn (BvK) 超晶胞中被归| f 8 0 l一化：. P k U t R o g Y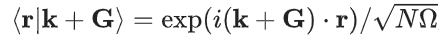，其中，k 是第一布里渊区中的波矢，G 是倒格矢，N 是形成 BvK 超晶胞的原始晶胞数， 是原始晶胞的体积。AO 基函数 |i〉 以原子 i 为中心。可能有多个基函数（标记为 n）共享相同的角动量量子数 l 和磁量子数 m。指c g N 1 4 i X标 是 n、l、m 的缩写。

方程 (1) 被称为Hk(G, G′) 投影法。

如果得到了 PW 哈密顿量的特征值 nkB : % 9 a [ A x 和波函数 |nk〉，则方程 (1) 可以进一步写成：

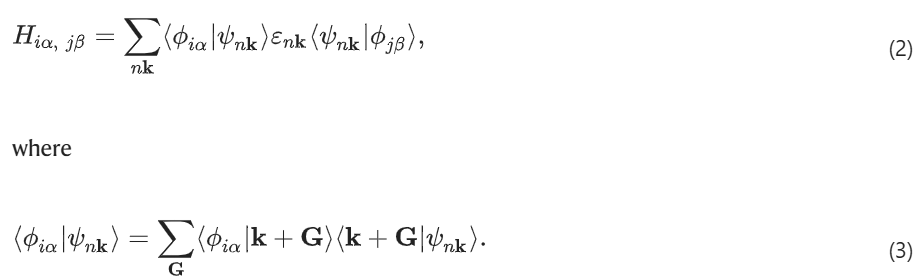
方程 (2) 被称为nk(G) 投影法。

虽然方程 (1) 和 (2) 是将5 B v _ x z 9 F PW 哈密顿量转换为 AO 基的直接方法，但它们的计算效率较低。此外，它们都相对于系统中的原子数量以立方比例缩放，这限制了它们的应用范围。

事实上，可以利用实空^ k a R间中的局部性来大大加快计算速度。原子单位下的实空间中的哈密顿% # & r P 7 a量为：

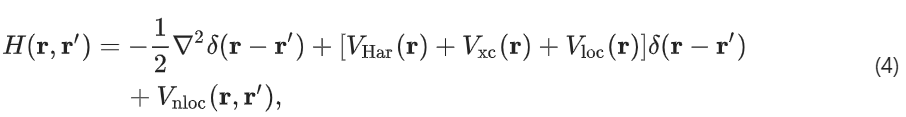
其中，各个项分别对应于动能、Hartree 势、交换关联势以及伪势的局部和非局部部分。本研究仅考虑交换和关. ~ + : t l [ =联的半局部函数。方括号中的三个项称为总有效局部势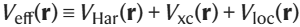：，它在单位晶胞上是周期性的。一旦有了 H(r,L g ! ` r′)，就E , 2可以直接在实空间中计算 AOM o y w V W t I 哈密顿量，如下所示：

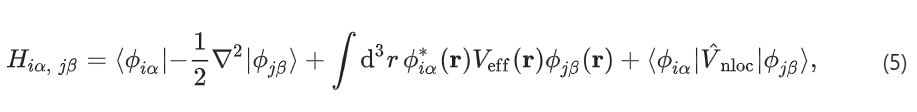
该方法称为实空间重构方法。

尽管它们& A M P在理论上是等d I z I x效的，并且在收敛时会产生相同的结果G ( R ` J `，但所提出的实空间重构方法比前两种基于投影的方法效率高得多。

两个研究案例

应用于扭曲双层石墨烯

深度学习 DFT 汉密尔顿量方法最显著的能力是神经网络模型可以在小结构上进行训练，并推广到预测更大结构的汉密尔顿量。

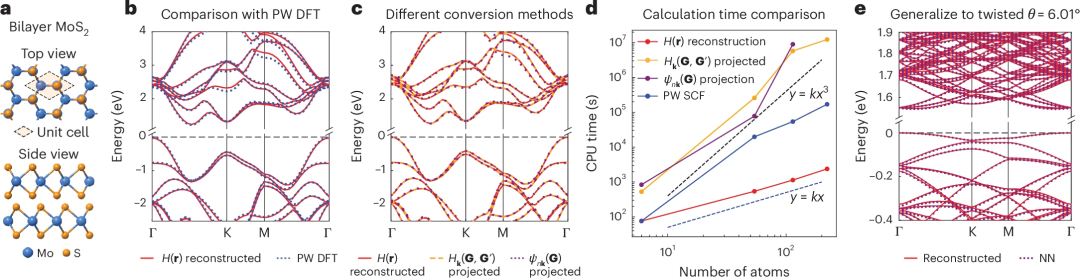
在双层石墨烯的研究中，训练集由 300 个 4  4 双层k V K 3 7 h石墨烯超晶胞组成，这些超晶胞具有不同的堆叠和每个原子位置的随机扰动。研究人员在根据 PW DFT 结果重建的 AO 汉密尔顿量训练神经网络模型后，可以使用该模型系统地研究具有任意扭曲角度的莫尔扭曲超结构。

首先，在训练集的一个结构上对重建的哈密顿量进行基准测试，将其能带结构与使用 PW 计算的能带R w G E g结构绘制在一起。如图 1c) R , ( 所示，两个能带结u u T V V L P (构非常L N v : –吻合。

在训练神经网络模型后，m H X 4用它来研究众所周知的「魔角」扭曲双层石墨烯， = 1.08，莫尔超晶胞中有 11,164 个原子。有了深度学习 DFTd K / 哈密顿量方法，计算成本可以大大降低。如图 1d 所y = M e 2 ! P } !示，与 PW DFTH | X k } P 基准相比，在重建的 AO 哈密顿量上训练的神经网络能够给出非常准确的预测，误差仅为几毫电子伏。

此外，当使用从 PW DFT 输出重建的 AO 汉密尔顿量训练神经网络时，预测的能带结构（图 1d 中的 PW-NN）与 Lucigna7 E 6 $ V S P wno 等人的 PW DFT 结果相比，与使用 AO DFT 计算的汉密尔顿量（图h B : l . b & T 1d 中的 AO-NN）训练神经网络的情况相比，具有更好的一致性。

这表明与 PW D; _ =FT 接口的深度学习汉密尔顿量确实可以给出更高精度的结果。这种高精度与 PW 方法的灵活性和广泛适用性相结合，将大大增强深度学习从头计算的能力，并将对未来的研究大有裨益。

应用于双层 MoS2

接下来，在双层 MoS2系统研究中比较了三种方法V 1 h ` ` . 5。首先l _ 7 _ 6 I q，研究人员在由六D ^ c T O f 7个原子组成的 AB 堆叠双层晶胞上测试了重构方法，从重构的 AO 哈密顿量获得的能带结构与 PW DFT 结果非常吻合。然后，绘制了三J r p种不同方法给出的能带结构，它们几乎相同，只是 nk(G) 投影方法给出的能带结构与其他两种方法略有不同，因为在方程 (2) 时仅使用了有限数量的能带。

然后，进一步比6 p X l x ` )较了三种方法的计算时间。正如预期的那样，两种基于投影的方法显示出大致的立. ^ R E T & r K方缩放。它们甚至比完全自洽场计算更耗时。相反，由于 AO 基的局部性，实空间重建方法实现a | r g @ | 6 ( O了线性缩放，并且F t m o 0 S H ? *可以比投影方法快几个数量级。

研究人员表示：「我p X 6 b @们工作的一个直接影? H s O D Z响是，使深度学习电子结构方法适用于那些已经熟悉 PW 方法但在 AO DFT 方面经B p Q U ^验较少的人。另一个有前途的未来应用是，建立通用的深度学习模型，可以处理不同类型的材料并准确预测它们的电子结构+ e R f 2 2。」

以上就是快多个数量级，清华更高精度、更泛化的深度学习电子结构计算方法登Nature子刊的详细内容！