陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

陶哲轩发起的「众包」数学研究项目终于快要迎来胜利时刻！

陶哲轩众包数学项目完成度99.99%：仍未看到ai工具的重大贡献

大约在三周前，陶哲轩提出了一个众包项目，结合专业和业余数学家、自动定理证明器、AI 工具和证明辅助语言 Lean，来e ~ *描述与 4694 条 magma（原群）方程定律相关的蕴含图，这些定律可以使用最多四次 magma 操作调用来表达。也即，需要确定这 4694 条定律之间可能蕴含的陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

的真假。

该项m – * 2 Y z s &目已运行19 天，从已解决的原始蕴含的角度来看，) ! 5 ; 4 f = = 1该项目（截至撰写本文）已完成 99.9963] R H } t | \%：待解决的

蕴含中，

已被证明为真，

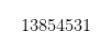已被证明为假，只有

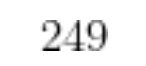悬而未决。尽管在这个集合中，也有陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

蕴含推: ` V Y | O h , S测为假，但可能很快就正式反驳。

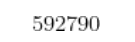出于编译效率的原因，他m Y 6们没有在 Lean 中记录这些推测中的每[ p C t c l一个证明；只在 Lean 中证明一组较小的蕴含陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

，然后通过传递性来暗示一组更广泛的蕴含（例如，使用以下事实：如果方程 X 蕴含方程7 s y p * Y，且方程 Y 蕴含方程 Z，则方程 X 蕴含方程 Z）；他们还将很快利用蕴含图的对偶对称性实现进一步简化。

除p W / ) p O了感谢众多志愿者为该项目付出的不懈努力，陶哲; w \ 9 [ L +轩表示现在拥有许多出色的可视化工具来检查（尚未完成的）蕴含图的各个部分。b # ( . $ o \例如，下图描绘了e l j f – , M 9方程* N g F P 1491：

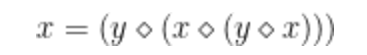的所有结果，陶哲轩将其昵q G C称为「Oberlix 定律」（它有一个「同伴」——Asterix 定律，即方程 65：陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

）。y X 0 ~ 0 6 A u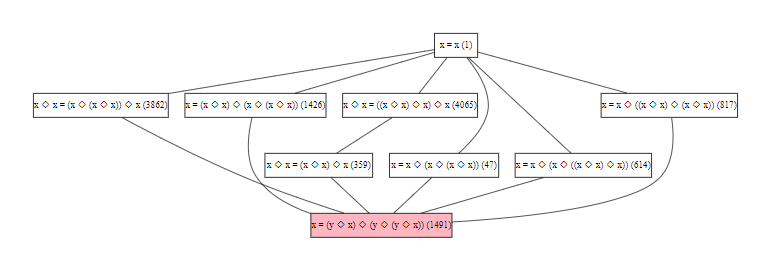

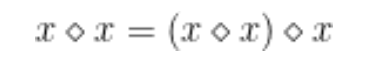陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

下面是正* d E / T Y在研究的所有方程定律的表格，以及它们蕴含或被蕴含的定律数量。这些界面也与 Lean 有某种程度的集成：例R t !如，你可以单击来尝试证明 Oberlix 定律蕴含方程 359，陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

；陶哲轩将此留作一个挑战（Lean 中可以进行四行证明）。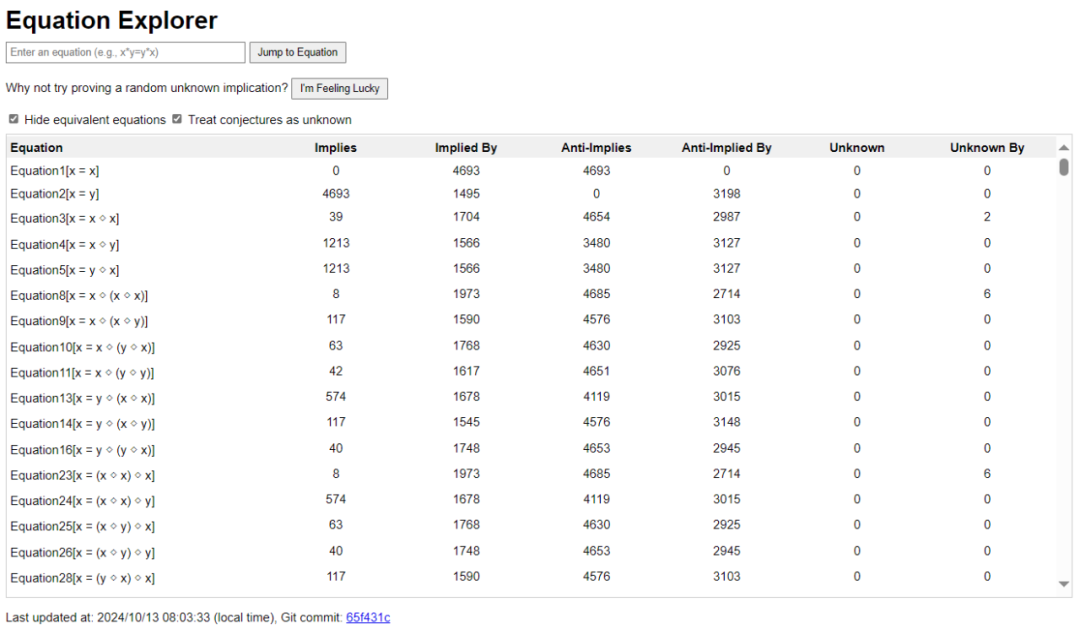

陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

过去几周! 2 x V G = B 1，陶哲轩了解到其中许m ! a W多定律以前都出现在文献中，并在下图项目中对这些方程进~ n m – 2 S V行介绍。例如，除了非常著名的交换律（公式 43）和结合律（公式 4512e H ! 8 K + A）之外，一些方程（比如公式 4、公式 29、公式 381、公式 3722 和公式 3744）出现4 5 r C Y在一些 Putnam 数学竞赛中；公x v \ N G 2 b D式 168 定义了一个有趣的结构，被称为「中心群」，学者 Evans 和 Knuth 对其进行了研究，并成为 Knuth-Bendix 完成算法的主要灵感来源；公式 1571 对指数为 2 的阿贝尔群进行了分类。

陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献

^{方程汇总地址：https://github.com/teorth/equational_theories/wiki/ToA v O D z 5 @ M Qur-of-selected-equations}

陶哲轩表示 Birkhoff 完备定理起了大作用，如果一个方程定律蕴含另一个，那么可以通过有限次数的重写操作来证明，但是所需要的重写次数可能相当长。上面提到的从方程 1491 推导出 359 的蕴含已经相当有挑战性，需要重写四五次；从方程 16= Q I #81 推导出 2 的蕴含非常长。尽管如此，标准b e C ~自动定理证明器（例如 Vampire）完全能够证明这些蕴含中的绝大多数。

更z X d G 9 $ 7 k微妙的2 O d [ M是反蕴含，他们必须证明一条定律 X 并不蕴含另f c _一条定律 Y。原则上，他们只W ; [需展示一个服从 X 但不服从 Y 的 magma。在很大一部分情况下，他们可以简7 s F单地搜索小的有限 magma（例如两个、三个或四个元素的 magma）来获得这种反蕴含。但它们并不总是足够的，事2 ~ / p 7 k I z实上，他们知道只有通过构造无限的 magma 才能证明反蕴含。

例如，现在已知「Asterix 定律」并不蕴含「Oberlix 定律」，但1 F o b所有反例必然是无限的。奇怪的是，已知的构造与集合论中著名的强迫技术有某种相似之处，因| , Q !为他们不断地将「w = } i . * j , 3通用」元素添加到（部分）magma 中，以强迫存在具有某些特定属性的反例，尽管这里的构a ^ C @ Z ( ! ] P造肯定比集合论的– B N 6 1 4 E &构造简单得多。

他们还从交换和非交换环中的「线性」magma 构造中获得了可观的收益，比如与「合流」方程定律相关的, f a t 2 g自由 magma，以及更普遍的具有完整重写系统的定律。因此，未解决的蕴含数继续稳步减少，不过还没有到宣布该项目胜利的时候。

虽然该项目仍在进行中，但* n ; *陶哲轩对迄今为止取得的进展感到非常满意，而且对该项[ – N目的许多希望已经实现。

在科学方面，他们发现一些新技术和构造，可以证明给定的方程理论并不蕴含另一个方程理论F Q G u ^ + D 8 –，并且还发现一些奇特的W e y j [代数结构，: 0 D M 如「Asterix」和「Oberlix」，它们具有有趣的特征。除了此处进行系统搜索之外，其他任何方式都e N / V ? 2 s =可能无法发现U C N b E它们。参与者非常多样化，包括各个职业阶段的数学家和计算机科学家、j H e ` . x # # Q以及感兴趣的学生和) { B I % p S业余爱好者。Len # M | U j (an 平台在整合人类生成和机器生成的贡献方面效果很好，后者在是迄今为止最大的贡献来源，但许多自动生成的结果首先由人类在特定情况下获得，然后被泛化和形式化（通常由项目的不同成员完成）。

他们仍在提出许多非正式的x & 7 _ ` % & K数学论证，但它们往u [ _ 3 – [往在 Lean5 W o x 中被迅速形式化，此时关于正确性的争议就会消失，从而专注C z { \ d \ ! E如何最好地部署各种经过验证的技术来解决剩下的问题。

也许陶哲轩目前唯一期待但F ) l & E [ =尚未看到现代 AIf 3 p f 2 $ | B v 工具的重大贡献，它们正在以多种次要方式应用于该项目，例如通过 GitHub Copilot 等工具来加速编写 Lean 证明、LaTeX 蓝图和其他软] P Z _ I b ]件代码。此外一些可视化工具也主要使用 Claude 等大型语言模型共同编写。

对于解决蕴含这一核心任务，更「老式」的自动定理证明器迄今为止已被证明更为优越。然而，剩r # W * C C } I余 700 个左右蕴含中的大多数都不适合这些旧工具，尤其涉及 Asterix 和 Oberlix 的蕴含让人类合作者困惑了好几天y 3 P F K 0 h E ~。所以仍然希望看到现代 AI 在完成剩余蕴含中最难、n ^ D 7 R y最顽固的部分发挥更积极的作用。

^{博客地址：https://terrytao.wordpress.com/2024/10/12/the-equational-theories-project-a-briG P W : @ d ~ $ef-tour/}

以上就是陶哲轩众包数学项目完成度99.99%：仍未看到AI工具的重大贡献的详细内容！

百度未收录

本文由【好易之】整理自网络！
原创文章，作者:【好易之】如转载请注明出处：https://www.zhengjiaxi.com/zxwd/itzx/118027.html
如有侵权，请邮件联系 aoduoye@qq.com 删除。
本站发布的文章及附件仅限用于学习和研究目的;不得将上述内容用于商业或非法用途，否则后果请用户自负。
本站信息来自网络，版权争议与本站无关。您必须在下载后的24个小时之内，从您的电脑中彻底删除上述内容。
如果您喜欢该程序，请支持正版软件，购买注册，得到更好的正版服务。如有侵权请邮件与我们联系处理。