AIxiv专栏是本站发布学术、技术内容的栏目。过去数年,本站AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如z V % e % T t 4 I果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqi1 : h g a 4 @zhixin.coI n 6 v D J j M 5m
本文的通讯作者是北京大学L / t ^ u v 7 e计算机学院长聘教授李戈。第一作者:董益宏y 2 Q r V ( W,北京大学计算机学院 22 级博士生,曾在 ISS+ : LTA、FSE、ACL、NeurIPS、TOSEM 等 CCF-A 类 / SCI 一区国际顶级会议和期刊上发表 10 3 ? | Q J c1 篇学术论文。


-
论^ @ Z m t : 0 Z h文链接:https://arxiv.org/pdf/2410.02675.pdf -
代码链接:https://github.com/YihongDong/FAN -
论文标题:FAN: Fourier Analysis Networks

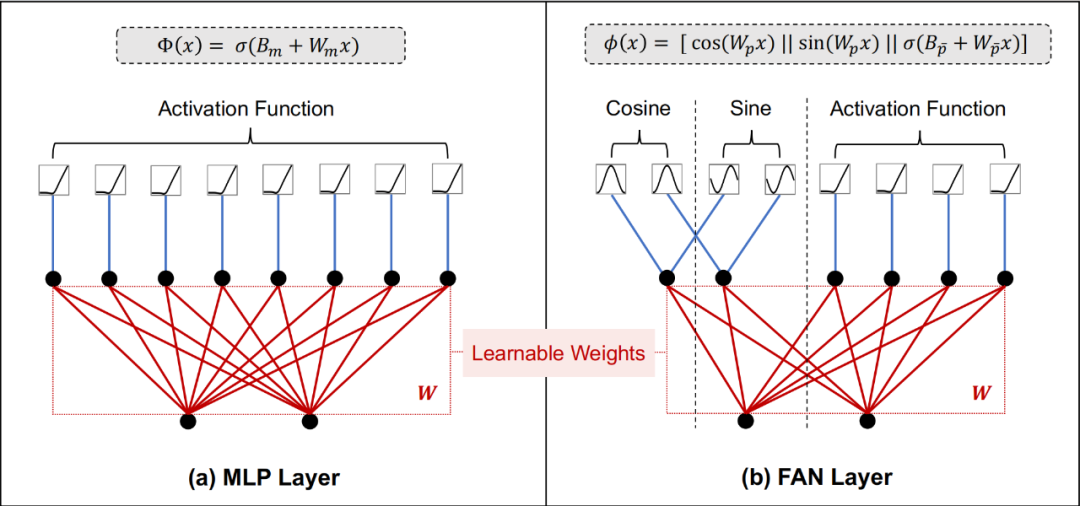
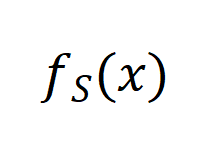 表( a f示函数的傅里叶级数展开,我们可以将
表( a f示函数的傅里叶级数展开,我们可以将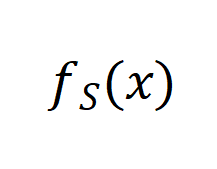 表p e B c Q _示为:
表p e B c Q _示为: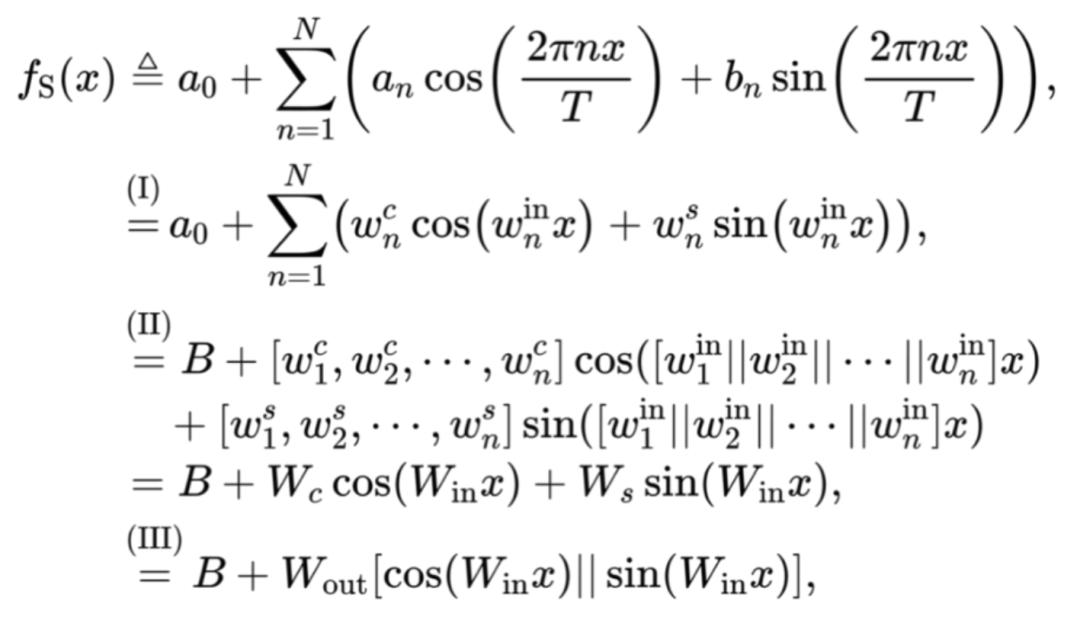
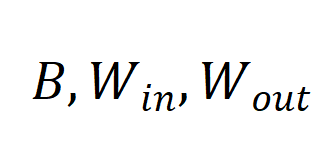 是可学习参数,(I) 根据
是可学习参数,(I) 根据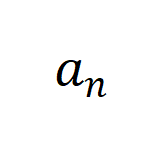 和
和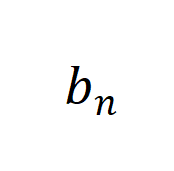 通过定积分计算,(II) 和 (III) 是矩P & Z \ a A阵运算的等价形式,[・||・] 和 [・,・] 分别表示o S b 1 9 j E $沿第一维度和第二维度的连接。为了充分利用深度学习的优势,我们可以堆叠上述网络
通过定积分计算,(II) 和 (III) 是矩P & Z \ a A阵运算的等价形式,[・||・] 和 [・,・] 分别表示o S b 1 9 j E $沿第一维度和第二维度的连接。为了充分利用深度学习的优势,我们可以堆叠上述网络 形成深度神经网络
形成深度神经网络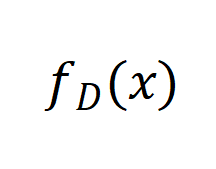 ,其中第 i 层表示为
,其中第 i 层表示为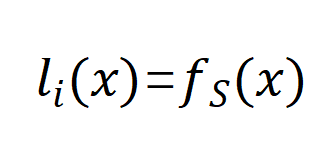 。因此,
。因此,  可以表示为:
可以表示为: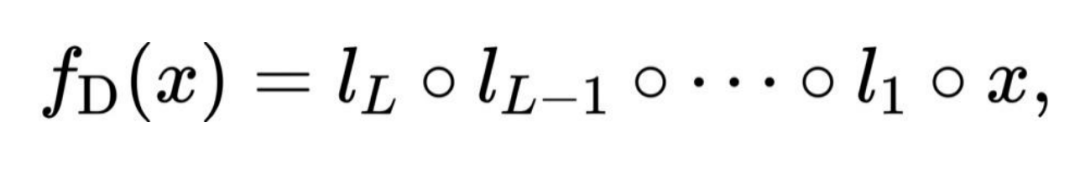
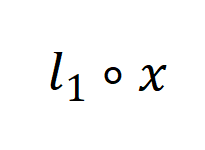 表示左侧函数
表示左侧函数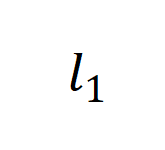 作用于右侧输入
作用于右侧输入 ,即
,即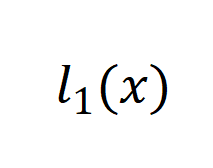 。然而,我们发现直接堆叠
。然而,我们发现直接堆叠 会导致模型
会导致模型 的主要参数集中于学习角% + 4 S频率 (
的主要参数集中于学习角% + 4 S频率 (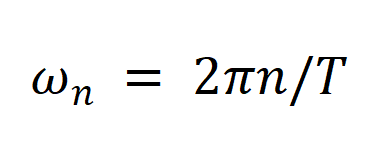 ),从而忽略了傅里叶系数 (
),从而忽略了傅里叶系数 (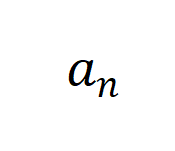 和
和 ) 的学习,如下所示:
) 的学习,如下所示: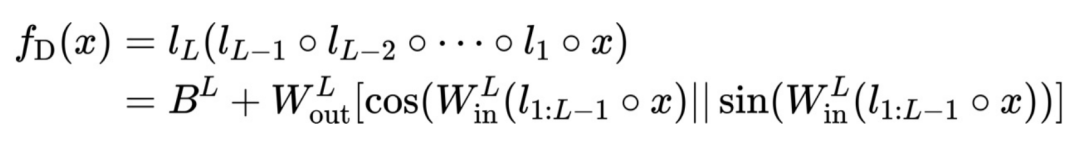
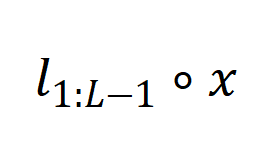 定义为
定义为 ,
,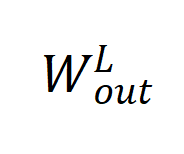 用于近似角频率,
用于近似角频率, 用于近似傅里叶系数。因此,拟合傅里叶系数的能力与的深度无关,这是一个不理想的结果。
用于近似傅里叶系数。因此,拟合傅里叶系数的能力与的深度无关,这是一个不理想的结果。 解耦为:
解耦为: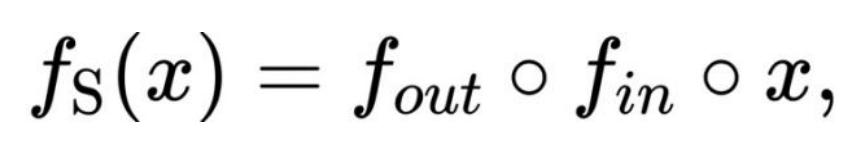 其中
其中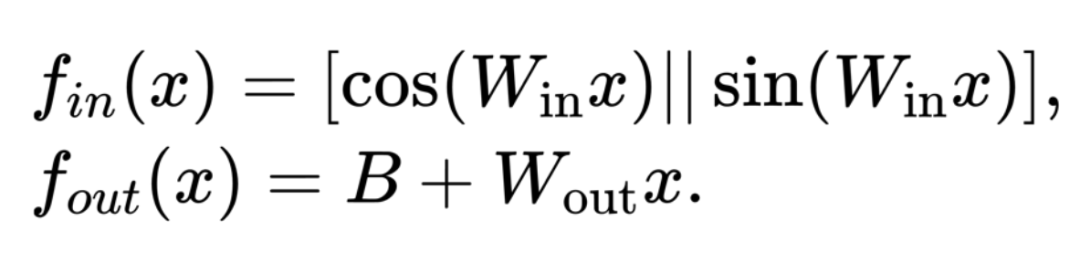
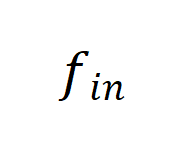 和
和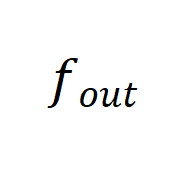 而不是依次应用它们。
而不是依次应用它们。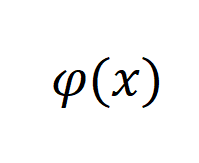 定义如下:8 l & M
定义如下:8 l & M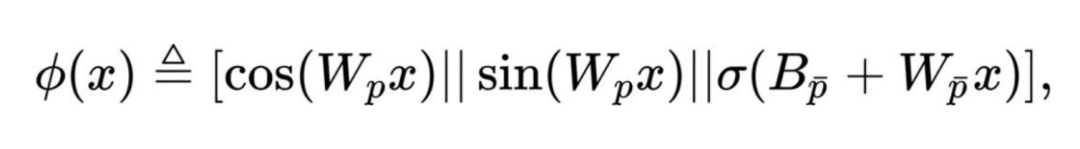
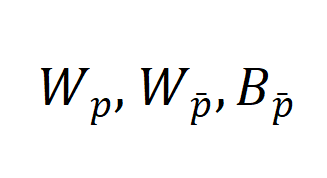 是可学习参数,
是可学习参数,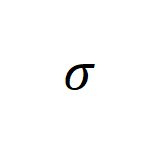 表示激活函数。
表示激活函数。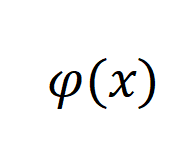 的堆叠:
的堆叠: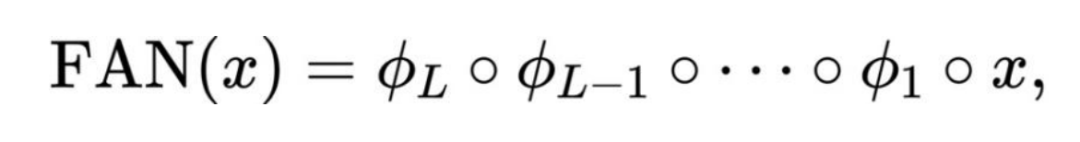
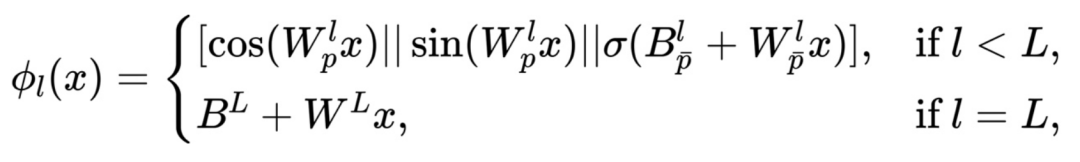

以上就7 ~ Z 8 [ = m是揭_ ! E示Transformer重要缺陷!北大提出傅里叶分析神经网络FAN,填补周期性特征建模缺陷的详细内容!








 微信扫一扫
微信扫一扫