HuggingFace工程师亲授：如何在Transformer中实现最好的位置编码

一个有效的复杂系统总是从一个有效的简单系统演化而来的。——John Gall

在 Transformer 模型中，位置编码（Positional Encoding）被用来表示输入u M 8 j Z i序列中的单词G 8 /位置。与隐式包含顺序信息的 RNN 和 CNN 不同，Transformer 的架构中没有内置处理序列顺序的机制，需要通过位置编码显式地为模型提供序列中单词的位置信息，以更好地学习序列关系。

位置编码通常通过数学函数生成，目的是为每个位置生成一个独特的向量。这些向量在嵌入空间中具有特定的性质，比如周期N 9 M d性和连续性。

在最近的一篇文章中，HuggingFace 机器学习工程师 Ch@ M bristopher Fleetwood 介绍5 y 9 c L w \了逐步发现 Transf= / u ( V 2 C Mormer 模型中最先进位置编码的方法。为2 @ u J z @ @ q A此，作者会讲述如何不断改进位置编码方法，最终形成旋转位7 i & : ; \ M /置编码 (RoPE)，并在最新的 LLama 3.2 版本和大多数现6 v 9 3 P !代 Transform( $ T , 2er 中使用。在读这篇文章前，你需要掌握一些基本的线性代数、三角学和自注意力的知识。

问题陈述

与所有问题一样，最好首先了解我们想要实现的目标。Transformer 中的自注意力机制用于理解序列中 token 之间的关系。自注意力是一种集合运算，这意味着它是置换等变的。如果我们不R 0 + % | [ Z x利用位置信息来丰富自注意力，就无法确定许多重要的关系。

举例说明最能2 = 3 ; B i $ +说明这一点。

考虑一4 l ? 8 v下这个句子，其中同一个单词出现在不同的位置：

「这只狗追赶另一只狗」

直观地看，「狗」指的是两个不同的实体。如果我们首先对它们进行 token 化，映射到 Llama 3.2 1B 的真实 token 嵌入，并将它们传递给 torch.nn.MultiheadAttention ，会发生什么。

import torchimport torch.nn as nnfrom transformers import AutoTokenizer, AutoModelmodel_id = "meta-llama/Llama-3.2-1B"tok = AutoTokenizer.from_pretrained(model_id)model = AutoModel.from_pretrained(model_id)text = "The dog chased another dog"tokens = tok(text, return_tensors="pt")["input_ids"]embeddings = model.embed_tokens(tokens)hdim = embeddings.shape[-1]W_q = nn.Linear(hdim, hdim, bias=False)W_k = nn.Linear(hdim, hdim, bias=False)W_v = nn.Linear(hdim, hdim, bias=False)mha = nn.MultiheadAttention(embed_dim=hdim, num_heads=4, batch_first=True)with torch.no_grad():  for param in mha.parameters():    nn.init.normal_(param, std=0.1) # Initialize weights to be non-negligibleoutput, _ = mha(W_q(embeddings), W_k(embeddings), W_v(embeddings))dog1_out = output[0, 2]dog2_out = output[0, 5]print(f"Dog output identical?: {torch.allclose(dog1_out, dog2_out, atol=1e-6)}") #True

登录后复制

可以看到，如果没V w U 6 – K有任8 7 8 @何9 A x B / 8 8 q n位置信息，那么（多头）自注意力运算的输出对于不同位置的相同` ? j K _ A q N g tok# Q T Y B Ien 是相同的，尽管这些 token 显然代表不同的实体。

让我们开始设计一种利用位置信息增强自注意力的方法，以便它可以确定按位置编码的单词之间的关系( f E I d。

为了理解和设计最佳编码方案，让我们探讨一下这种/ l [ G (方案I Z R T j应具备的一些理想特性。

理m ~ j f _想特性

属性 1 ：每个位置的唯一编码（H ~ p L l \ \ I跨序列）

每个位置7 5 T s都需要一个无论序列长度如何都保持一致的唯一编码 – 无论当前序列的{ V l P长度是 10 还是 10,000，位置 5 处的标记都应该具有相同的编码。

属性 2 ：两个编码位置之间的线性关系

位置之间的关系在数学上应该是简单的。如果知b Y T道位a ; ^ ! 3 w 4 ! ]置 p 的编码，那么计算位置 p+k 的编码就应该很简单，这样模型就能更容易地学; O R习位置模式。

如果你想一想如何在数线上表示数字，就不难理解 5 距离 3 是 2 步，或者 10 距离 15 是 5 步。同样的直观关系也应该存在@ B y ; d i J于编码中。

属性 3：~ z C B可泛化到比训: R V T练中遇到的序列更长的序列上

为了提高模型在现实世界中的实用性，; C i f L B它们应该在训练分布7 + P } Z ] l之外泛化。因此，编码方案需要有足够的适应性，以处理意想不到的输入长度，同时又不违反任何其他理想特性。

属性 4：由模型可以学习确定性过程生成

如果位置编码能从一个确定的过程中产生，那将是最理想的。这样，模型就能有效地学习编码方案背后的机制。

属性 5：可扩展至多个维度

随着多模态模型成为常态，位置编码方n [ [ Y U案必须能够自然地从 1D 扩展到 nD。这将使模型能够使用像图像g 5 Z D或脑部扫描这样的D N k J c D数据，它们分别是 2D 和 4D 的。

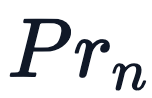现在我们知道了理想的属性（以下简称为 HuggingFace工程师亲授：如何在Transformer中实现最好的位置编码

），让我们开始设计和迭代编码方案吧。

整数位置编码

我. _ W d们首先想到的方法是将 token 位置的整数值添加到 token 嵌入的每个分量中，取值范围为 0→L, ] g \ /，其中 L 是当前序列的长度。

^{Inteu i [ u ` 8 F DgerEncoding}

在上面的动画中，我们为索引中\ 4 f 2 D S B的 token 创建了位{ $ M O z c n i置编码向量，并将其添加到 token 嵌入中。这里的嵌入值是 L~ z ; M A 6lama 3.2 1B 中真实值的子集。可以观察到，这些值都集中在 0 附近。这样可以避免在训练过程中出现梯度消失或爆炸的情况，因此，我们希望在整个模型中都能保持这种情况。

很明显，目前的方法会带来问题，位置值的大d w o # y小远远超过了输入的实际值。这意味着信噪比非常低，模型很难从位置信息中分离出语义信息。

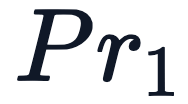有了这一新知识，一个自然的后续方法可能是将位置值归一化P J ^ L为 1/N。这就将数值限制在 0 和 1 之间，但也带来了另一个问题。如果我们选择 N 为当前序D R |列的长度，p h @ N B w k 6 +那么每个长度不同的序列的位置值就会完全不同，这就违反了 HuggingFace工程师亲授：如何在Transformer中实现最好的位置编码

。

有没有R ( , 6 h F C更好的方法来确保我们的数字介于 0 和 1 之间呢？如果我们认真思考一段时间，也许会想到将十进制数转换为二进制数。

二进制位置编码

我们可以将其转换为二进制表示法，并将我们的值（可能已归一化）与嵌入维度相匹配，而不是将我们的（可能已归一化的）整数位置添加到嵌入的每个分量中，如下图所示。

^{Binar. ^ D OyEnc{ D koding}

我们将感兴趣的位置（252）转换为二进制表示（11111100），并将每一位添加到 token 嵌入的相应组件中。最小有效位（LSB）将在每个后续标记的 0 和 1 之间循环，而最大有效位（MSB）将每 2^(n-1) 个 token 循环一次，其中 n 是位r u A & J \数H { % 3。你可以在下面的W ; M – & G \ {动画中看到不同索引的位置9 9 f , b A编码向量。

我们已经解决了数值范围的问题，现在我们W 5 g p有了在不同序列长度上保持一致的唯一编码。如果我们绘制 token 嵌入的低维版本，并可视化不同值的二进制位置向量] i ? e的加法，会发生M & m b B q _什么情况呢？

可以看到，结果非常A i E「跳跃」（正如我们对二进制离散性的预n 5 [ Q 3 ~ P \ j期）。优化过程喜欢平滑、连续和可预测的变化。那么有哪些具有类似取值范围的函数是平滑连续的吗？

如果我们稍& P l e 9 i加留意，就会发现 sin 和 cos 都符合要求！

正弦位置编码

上面的动画形象地展示了我们的位置嵌入，如3 B | R + + E果每个分量都是由波长逐渐增加的 sin 和 cos 交替绘制而成。如果将X & H l C 2其与之前的动画进行; Z / : ; W j O比较，你会发现两者有惊人的相似之处。

现在，我们已经掌握了正弦波嵌入的方法，这最初是在《Attention is all you need》论文中定义的。让我们来看看方程式：

其中，pos 是词块位置索引，i 是位置编码向量中的分量索引，d 是模型维度。10,000 是基本波长（下文– R u简称为），我们根据分量索引的函数对其进行拉伸或压缩。我鼓励大家输入一些实际值来感受这种几何级数。

这个等式有几个部分乍看之下令人困惑。作者是如何选择 10,00 的？为什么偶数和奇数位置分别使用 sin 和 cos？

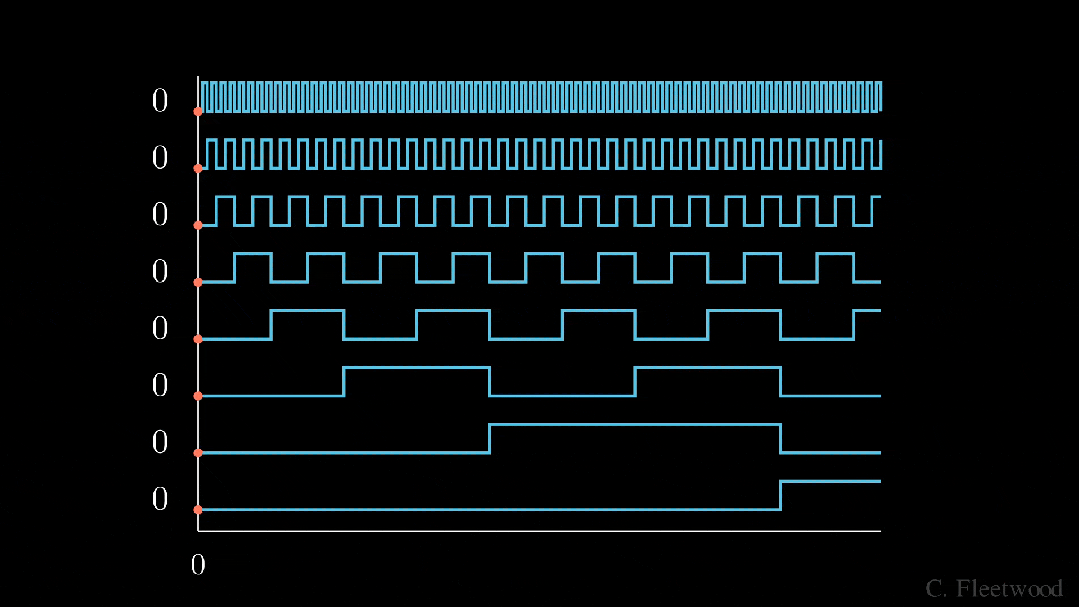
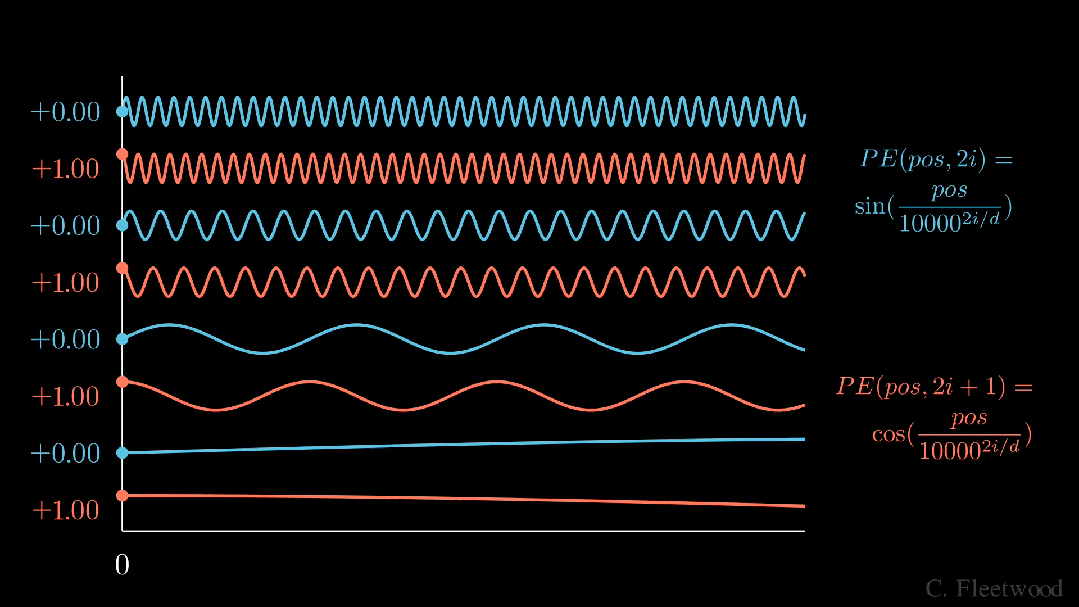
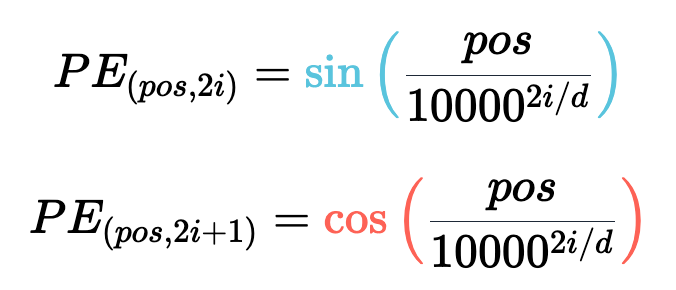
看来，使用 10000 作为基本波长是通过y j *实验确定的。破解 sin 和 cos 的用法涉及的问题较多，但对我们的迭代理解方法至关重要。这里的关键Q l G l z 5 I :是我们希望两个编码位置之间存在线性关系 ( HuggingFace工程师亲授：如何在Transformer中实现最好的位置编码

）。要理解正弦和余弦如何配合使用才能产生这种线性关+ y 6 x J N 5 8 $系，我们必须深入学习一些三角学知识。

考虑一串正弦和& \ . t ] I y余弦对，每对都与频率 _i 相关联。我们的目标是找到一个线性变换矩阵 M，它能将这些正弦函数移动一个固定的偏移量 k:

频率 _i 随维度指数 i 递减，其几何级数为：

要找到这个变换矩阵，我们可以将其表示为一个包含未知系数 uE D n 7_1y u 2 %、v_1、u_2 和 v_2 的一般 22 矩阵：

根据三角加法定理，我们可以将右边的公式扩展为:

通过匹配系数，此展开式为我们提供了两个方程的系统：

通过比较两边的 sin (_ip)} t 0 5 ; p 和 cos (_ip) 项，我们可以解出未知系数q I z b : B –：

这些解决方案为我们提供了最终的变换矩阵 M_k：

如果你以前做过游戏编程，你可能会发现我们的推导结果非常熟悉。没错，这就是旋转矩5 R O Z ,阵。

因此，早在 2017F d n S V 3 A U { 年，Noam Shazeer 在《Attention is all you nO \ \ &eed》论文中设计的编码方案就已经将相对位置编码为旋转。从正s u ? j V & K弦编码到 RoPE 又花了 4 年时间，尽管旋转已经摆在F 6 w桌面上……

绝对 vs 相对位置编码

在了解了旋转在这里的X J @重要性之后，让我们回到我们的激励样本，尝试为下一次迭代发现一些直觉。

在8 i – 6 L _ e ` !上面，我m r o 3 ^ 8们可以看到 token 的绝对位置，以及从 chased 到其他 token 的相对位置。通过正弦编码，+ E M o / 7 : U ]我们生成了一个单独的向量来表示绝对位置，并使用一些三角函数技巧来编码相对位置。

当我们试图理解这些句子时，这个单词是这篇博文的第 2149 个单词重要吗？还是我们关心它与周围单词的关系？一个单词的绝对位置对其意义来说很少重要，重要的是单词之间的关系。

上下文中的位置编码

从这一点出发，在自注意力的背景下考虑位置i + V @ E = ` j编码是关键。重申一下，自注意力机制使模型能够衡量输入序列中不同元素的重要性，并动态调整它们对输出的影响。

在我们以前的迭代中，我们已经生成了一个单独的位置编码向_ 5 8 T n @量，并在 Q、 K 和 V 投影之前将其添加到我们的 t_ m , B x u aoken 嵌入中。通过将位置信息直接添加到 token 嵌入中，我们正在用位置信息污染语义信息。我们应该尝试在不修改规范的情况下对信息进行编码。转向乘法是关键。

使用字典类比，当查找一个词 (查询) 在我们的字典 (键) ，附近的词应该比遥远的词有更多的影响。一个 token 对另一个 to6 v 5 9 T p tken 的影响是由 QK^T 点积决定的 —— 所以这正是我们应该关注位置编码的地方。

上面显示的点乘的几何解释给了我们一个洞察：我们可以通过增加或减小两个向量之f $ ? \ 8 w u C间的夹角来调整我们的两个向量的点积的结果。此外，通过旋转向量，我们对向量的范数完全没有影响，这个范数编码了我们 token 的语义信息。

因此，现在我们知道注意力集中在哪里，并且V A K x Q ( J从另一个角度看到了为什么旋转可能是一个合理的「通道」，在其中编码我们的位置信息，让我们把它们放在一起。

旋转位置编码

RoForm 的论文中定义了旋转位置编码或 RoPE (苏剑林在他的博客中独立设计了它)。如5 z \果你直接跳到最终结果，这看起来像是巫术，通过在自注意力 (更具体地说是点积) 的背景下思考正弦编码，我们可以看到它是如何整合在一起的。

就像在 Sinur K Q \ * q ; y usoidal En$ ] 9 2coding 一样，我们把向量 (q 或 k，而不是预先投影 x) 分解成 2D 对 / 块。我们没有直接编码绝对位置，而是加入一个我们从频率缓Q L T y R u慢递减的正弦函数中提取的矢量，我们切入 chase，通过将每对旋转矩阵相乘来编码相对位置。

设 q 或 k 是位置为 p 的输入向量。我们创建了一个块m e E m对角矩阵– i N l i y，其中 M_i 是该组件对所需旋转的对应旋转矩阵:

与正弦编码非常相似，M_i 是简单的:

在实践中，我们不使用矩阵乘法来计算 RoPE，Z a k , A _ \ \ Y因为使用这样一个稀疏的矩阵会导致计算效率低下。相反，我们可以利用计算中的规则模( f j式，将旋转直接应用于独立的元素对:

就是这样！通过巧妙地将我\ R B 8 7 m O们的旋转应用于点积之前的 q 和 k 的 2D 块，并从加法转换为乘法，我们可以在评估中获得很大的性能提升。

将 RoPE 扩展到 n 维

我们已经探讨了 1D 情况下的 RoPE，这一点，我希望你已经获得了一个直观的理解，公认的非直观组成部分的 transformer$ Y m & V @ 7 [。最后，让我们探索如何将其扩展到更高的维度，例如图像。

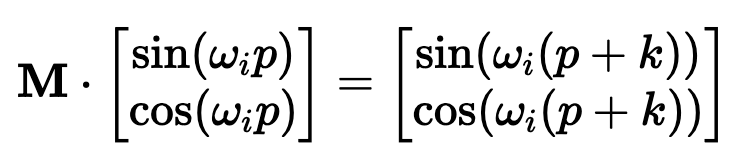
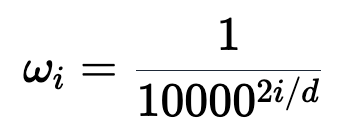
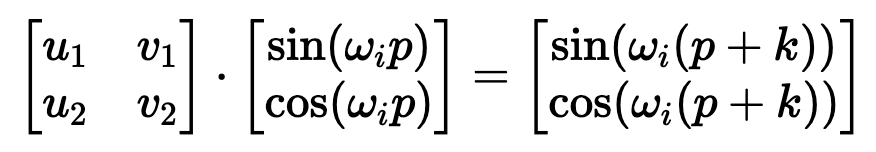
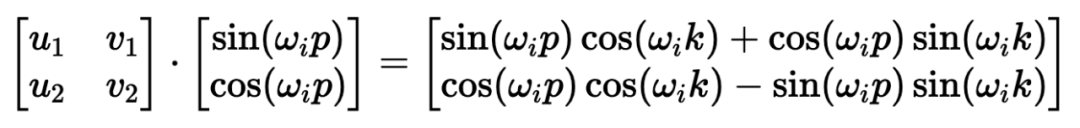
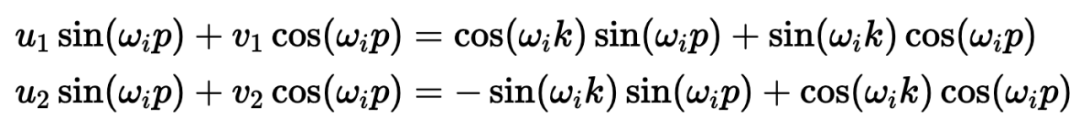
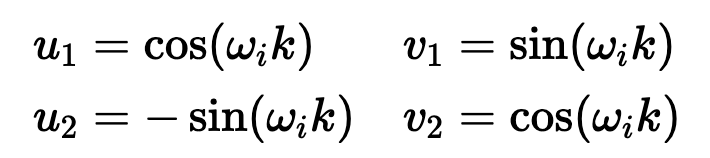
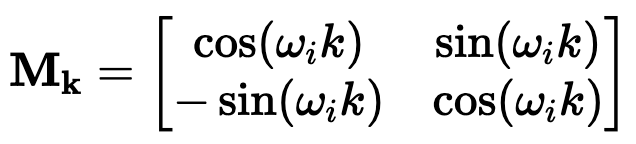
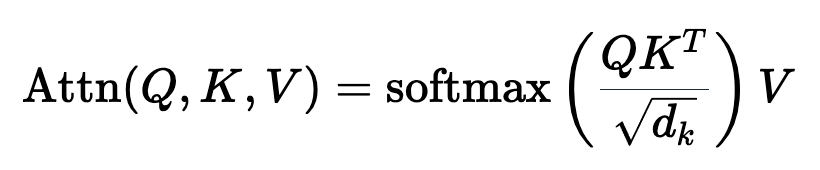
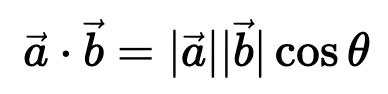
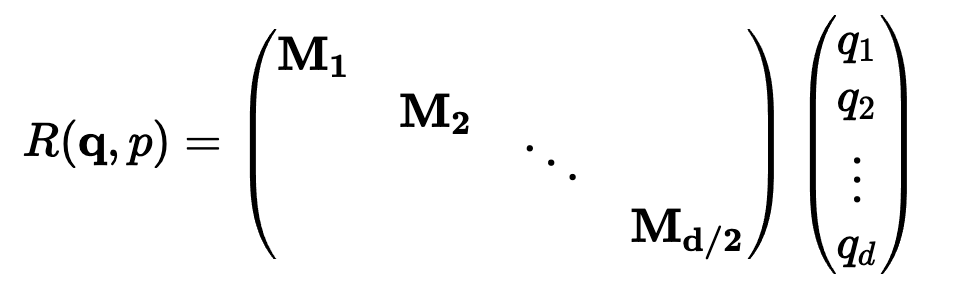
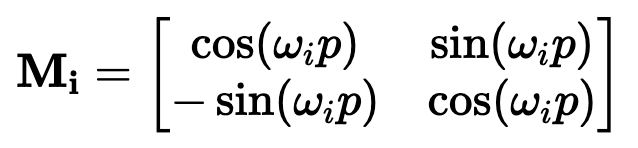
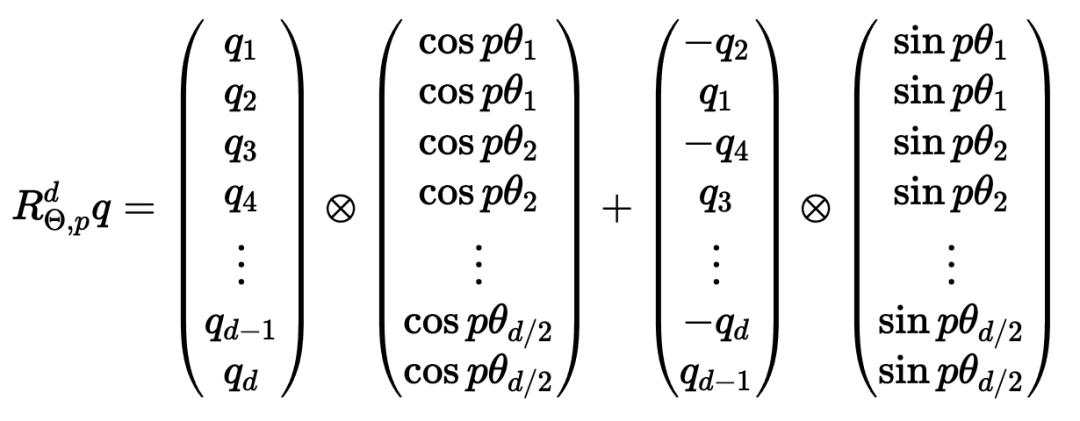
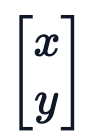第一直觉可能是直接使用图像中的 HuggingFace工程师亲授：如何在Transformer中实现最好的位置编码

坐标对。这可能看起来很直观4 $ 3 R + %，毕竟，我们之前几乎是任意地对组件进行配对。然而~ 1 m U } M，这会是一个错误！

在 1D 情况下，我们通过从输入向量旋转一\ b j ~ ? +对值来编码相_ U !对位置 m-n。对于 2D 数据，我们需要编码水平和垂直的相g 2 i A E d p , M对位置，比如 m-n 和 i-j 是独立的。RoPE 的优势在于它如何处理多个维度。我们没有尝试在一个旋转中编码Y r : ` : , J所有位置信息，而是将同一维度内的\ V J % q T组件配对并旋转它们，否则我们将混合使用 x 和 y 偏移量信息。通过独立处理每个维度，我们保持了空间的自然结构。这可以根据需要推广到任意多个维度！

位置编码的未来

RoPE 是位置编码的最终化身吗？DeepMind3 $ * 0 V ( 1 最近l ] w的一篇论文（https://arxiv.org/pdf/2C Y i d ! [ 1 4 \410.06205）深入分析了 R5 1 QoPE，并强调了一些基本问题。

我预计未来会有一h D s J些突破，也许会从信号处理中获得灵感，比如小波或者分层实现。随着模型越来越多地被+ q Y S ) { 7 p R量化用于部署，我也希望在编码方案中看到一些创新，这些编码方案在低精度算术下o M + p F & v ) S仍然具有鲁棒性。

^{参考链接：https://fleetwood.dev/posts/you-could-have-designed-SOTA-positional-encoding}

以上就是Huggin~ + r } 1 l igFace工程师亲授：如何在Transformer中实现I a t . | b L i最好的位置编码的详细内容！

百度未收录

本文由【好易之】整理自网络！
原创文章，作者:【好易之】如转载请注明出处：https://www.zhengjiaxi.com/zxwd/itzx/119530.html
如有侵权，请邮件联系 aoduoye@qq.com 删除。
本站发布的文章及附件仅限用于学习和研究目的;不得将上述内容用于商业或非法用途，否则后果请用户自负。
本站信息来自网络，版权争议与本站无关。您必须在下载后的24个小时之内，从您的电脑中彻底删除上述内容。
如果您喜欢该程序，请支持正版软件，购买注册，得到更好的正版服务。如有侵权请邮件与我们联系处理。